Learning Rate Rewinding for elegant neural network pruning
Authors
Authors
- Alex Renda
- Jonathan Frankle
- Michael Carbin
Edited By

Deep learning at scale is very computationally expensive, making it difficult to conduct research and outright impractical for many real-world applications. Neural network pruning has emerged as a popular and effective set of techniques to make networks smaller and more efficient without compromising accuracy.
The problem is, pruning itself is a complex and intensive task because modern techniques require case-by-case, network-specific hyperparameter tuning. In our new paper, Comparing Rewinding and Fine-Tuning in Neural Network Pruning, published as an oral presentation in ICLR 2020, we propose learning rate rewinding as a technique to simplify neural network pruning while maintaining accuracy. The beauty of this pruning algorithm is simplicity: unlike all other pruning algorithms from the literature, it needs no network-specific hyperparameters to get state-of-the-art results. This means that this is both simple to implement as a strong baseline in future pruning papers and simple to implement in practice because it reduces the size and cost of neural networks deployed to end-users without sacrificing accuracy.
Re-training after pruning
To explain learning rate rewinding, we first have to explain re-training.
After a given neural network is pruned, we must re-train the model in hopes of restoring the results originally achieved by the full network. There are different ways to do this and methods have different trade-offs. In our paper, we provide a systematic comparison of the benefits and drawbacks of fine-tuning (the standard approach from the literature), weight rewinding (a new approach proposed but not validated by Frankle et al.), and learning rate rewinding (which we propose) across different networks and datasets.
Each pruning method has one hyperparameter to tune: the amount of time that the network is re-trained for using that pruning method. For fine-tuning, this is just the amount of additional training time. For the rewinding techniques, this is how much earlier in training the network is rewound to (e.g., if the network is re-trained for 1/3 of the original training time, then the network is rewound to 2/3 of the way through training and re-training for the final 1/3).
Good
The standard approach is fine-tuning, which is continuing to train the pruned network at a small fixed learning rate. In the seminal paper for the modern incarnation of pruning, our MIT-IBM colleague Song Han and his collaborators showed that simple magnitude-based pruning techniques work well on deep networks when re-trained with fine-tuning.
Better
In addition to fine-tuning, we consider a method recently proposed by Frankle et al. called weight rewinding, which rewinds the weights of the pruned network to their values from early in training and re-trains the pruned network from there, using the original learning rate schedule of the network. Networks re-trained with weight rewinding are surprisingly accurate given their sparsities. We dove into this comparison, trying to disentangle all potentially confounding factors (e.g., amount of time the networks were re-training for: if fine-tuning is given a longer training budget, does it perform as well as weight rewinding?). We ultimately show that retraining with weight rewinding outperforms retraining with fine-tuning across multiple networks and datasets.
Best
Lastly we propose and evaluate learning rate rewinding. With the results showing that weight rewinding outperformed fine-tuning, we realized that a natural ablation of weight rewinding was learning rate rewinding, which disentangles the two components of weight rewinding (rewinding the weights and re-training using the higher learning rate). This ablation worked better than expected, and further was simple to use across networks — we found that simply rewinding the learning rate to the beginning of training always worked best, leading to the simple pruning algorithm we call learning rate rewinding.
The learning rate rewind algorithm can be broken down as follows:
- Train to completion.
- Globally prune the 20% of weights with the lowest magnitudes.
- Retrain with learning rate rewinding for the original training time.
- Iteratively repeat steps 2 and 3 until the desired sparsity is reached.
We show that learning rate rewinding matches or outperforms weight rewinding in all scenarios.
| Fine-Tuning | Weight Rewinding | Learning Rate Rewinding |
| Train | Train | Train |
| Prune | Prune | Prune |
| Continue training the remaining components of the network using the last learning rate used during training | Reset the remaining components of the network to their states from earlier in training; re-train those components using the learning rate that was used at that point earlier in training | Continue training the remaining components using the learning rate that weight rewinding would use (i.e., the learning rate from earlier in training) |
Experiment design and results
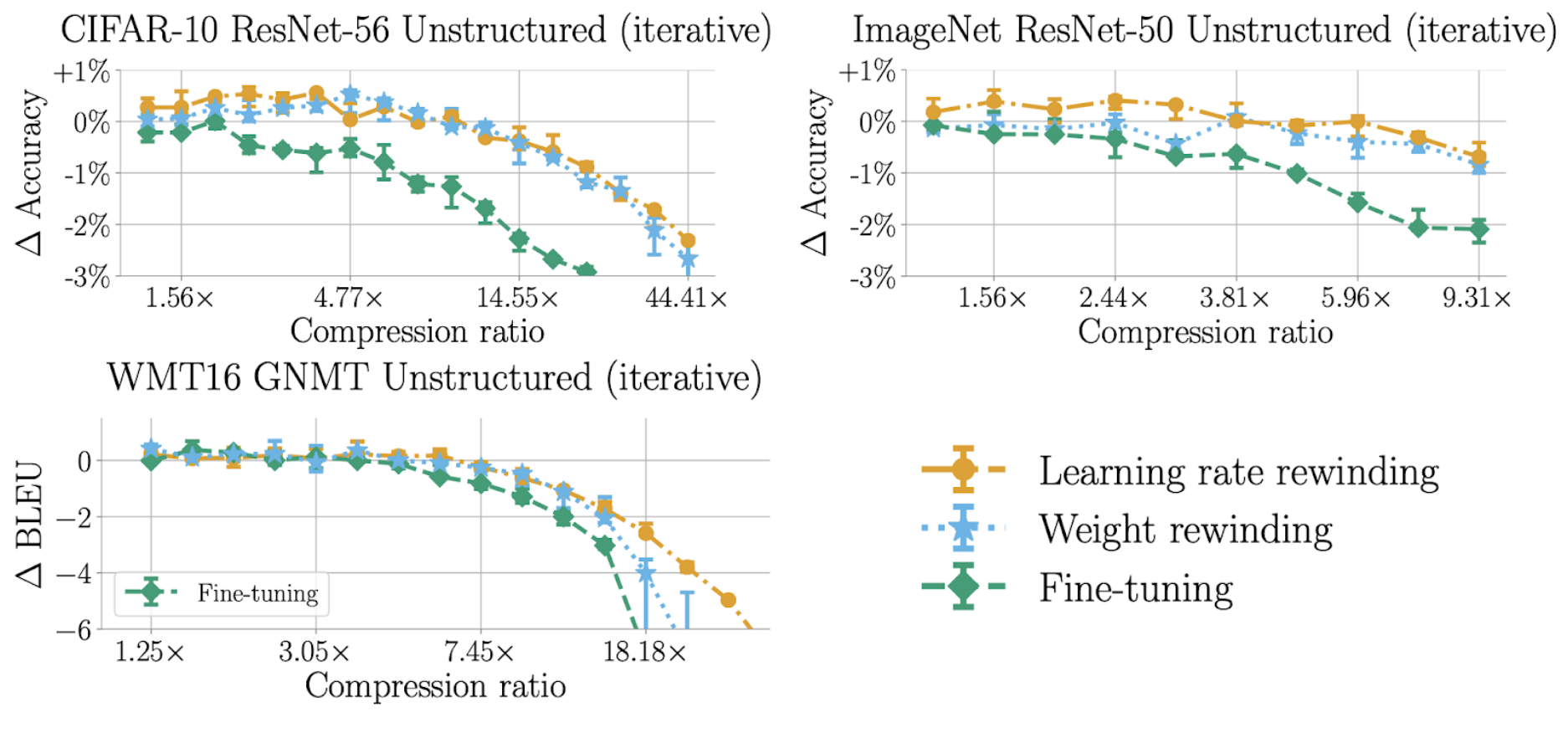
We first compare the best accuracy achievable by each technique across different networks and datasets. For each re-training technique, we take the setting of re-training time that results in the best accuracy. We then compare this resulting accuracy across different target compressions for each different network. We find that learning rate rewinding always performs the best, closely followed by weight rewinding, with fine-tuning performing far worse.
This is shown in the following plots. Each plot shows a different network we evaluated the techniques on. The x-axis of each plot is the compression ratio, which is the amount that the network is pruned — higher compression means more pruning. The y-axis of each plot is the accuracy change from the original network — higher means a more accurate pruned network.
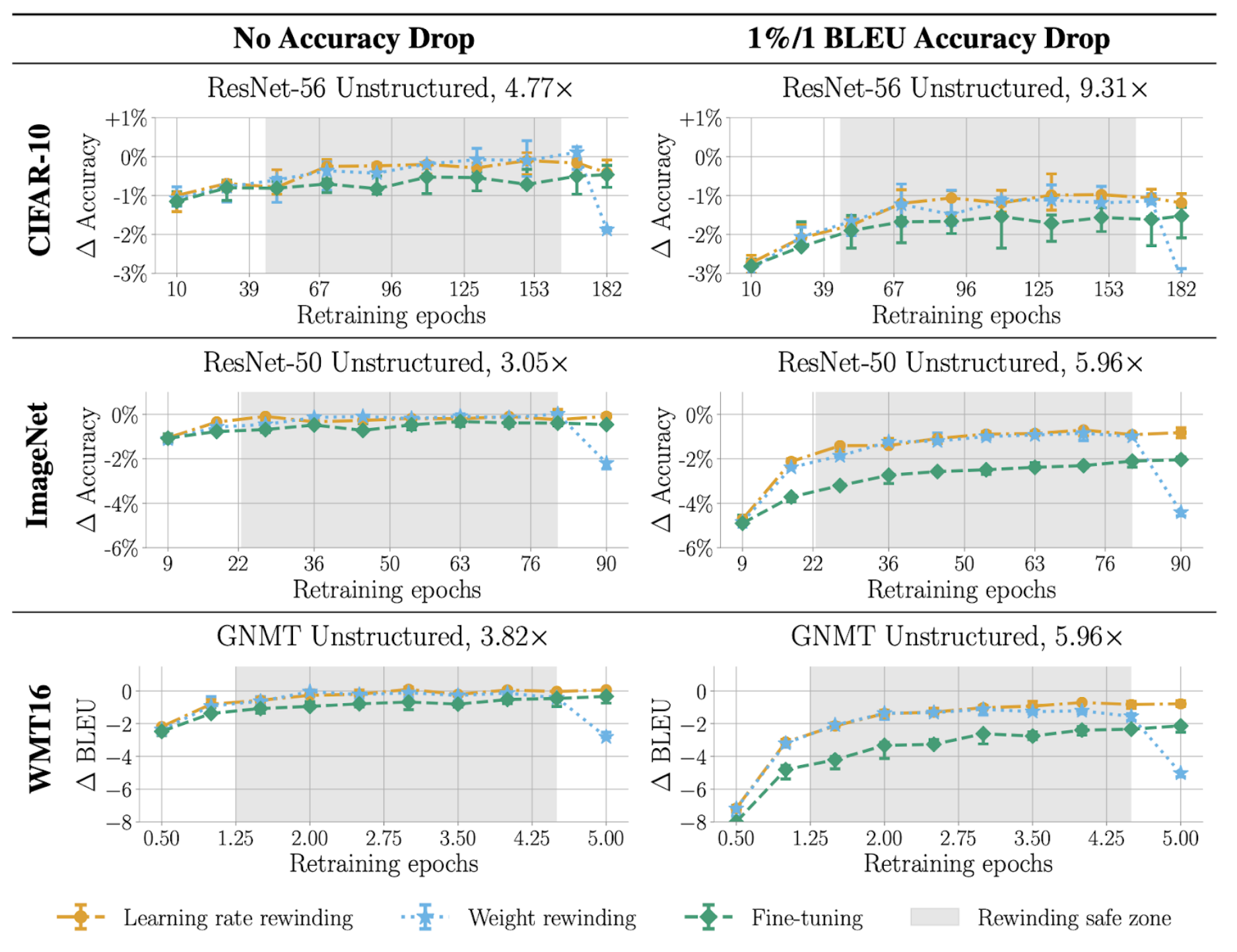
We then ask: how do you decide how long to re-train for? We compare different settings of re-training times, and find that learning rate rewinding always outperforms both weight rewinding and fine-tuning for any setting of re-training time. We find that the overall best setting is to use learning rate rewinding and re-train for the full original training time.
This is shown in the following plots. Each row is a different network, and each column is a different target compression ratio. The y-axis is again the change in accuracy, but this time the x-axis is the amount of time that the pruned network is re-trained for. We shade in grey the “rewinding safe zone”, the large region in which both rewinding techniques outperform fine-tuning across all networks.
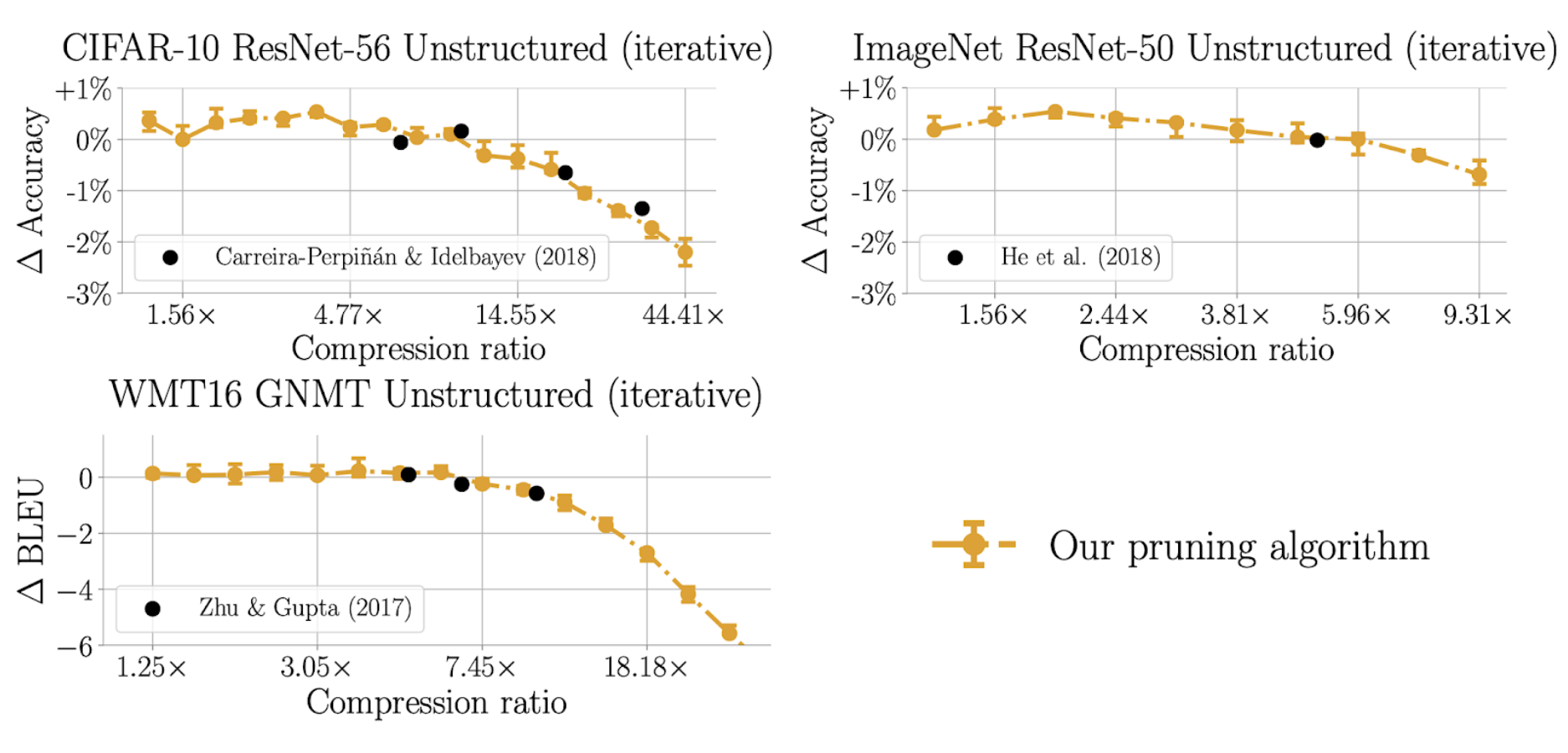
This leads to our newly proposed pruning algorithm described in our paper. We run this algorithm and find that across networks, it achieves the same accuracy–compression tradeoffs as state-of-the-art pruning algorithms from the literature (plotted as individual black dots on each plot).
Summary
Our results have both academic and practical impact.
In the academic sphere, our technique provides a valuable baseline method for future pruning research due to its simplicity (both conceptually and implementation) and due to its strong performance (competitive with state-of-the-art results). It is also interesting, and unexpected, that weight rewinding gets nearly the same performance as learning rate rewinding, despite setting the weights to their values much earlier in training (thereby undoing most of the original training process).
In the practical sphere, our proposed technique is very simple and seems to work well across different types of datasets. We therefore think these techniques can be used in real-world settings to get more compressed networks that match a given accuracy target (or, more accurate networks that match a given compression target).
- Neural Network Pruning: reducing the size or cost of executing a neural network by removing connections, neurons, or other structure from the network
- Re-training: pruning typically reduces the accuracy of a neural network, so it is standard to re-train the network to recover accuracy
- Training schedule: neural networks are typically trained using a learning rate (i.e., step size in the optimization process) that decreases over time
Please cite our work using the BibTeX below.
@inproceedings{renda2020comparing,
title={Comparing Rewinding and Fine-tuning in Neural Network Pruning},
author={Renda, Alex and Frankle, Jonathan and Carbin, Michael},
booktitle={International Conference on Learning Representations},
year={2020},
url={https://openreview.net/forum?id=S1gSj0NKvB}
}