A primer on causal graph intervention

In causal inference, interventions may be characterized as structural (“hard”) or parametric (“soft”). An example of hard intervention is a Randomized Control Trial (RCT), in which subjects are assigned to a treatment or a control group; here the randomization is a structural determinant of the distribution.

The control-versus-treatment scenario acts as an “on-off” switch that changes the structure of the graph by adding-removing a directed edge, thus allowing us to remove the confounding effect of a given exogenous variable.

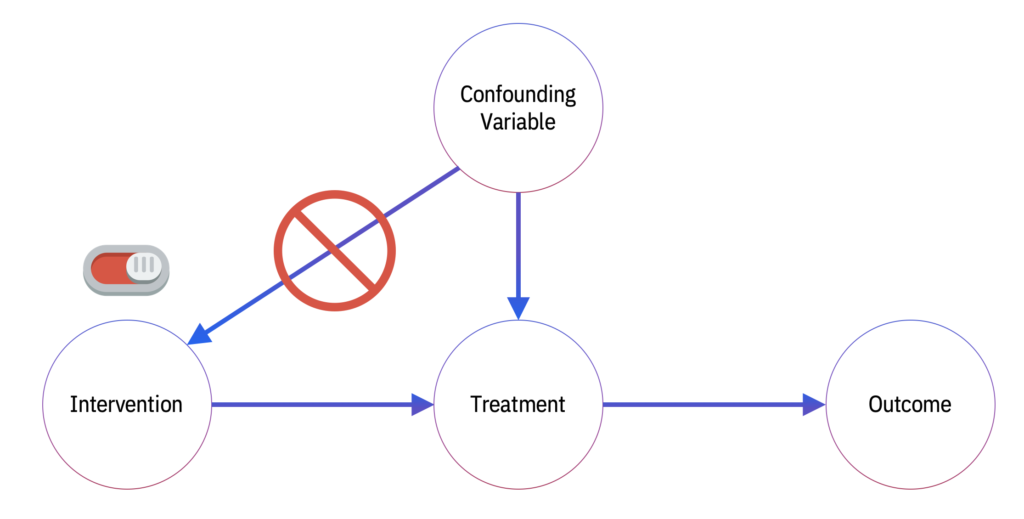
“Soft” interventions take a different approach. Rather than removing the edge, changing the structure of the graph, we instead modify the conditional probability distributions of the intervened upon variable. Thus when the intervention is set to “on,” the distribution of the variable conditional on the parent nodes changes but the casual edge itself is left intact. Soft-interventions are widely employed in biology and medicine, where it is hard to cut off parental influences, but possibly easier to perturb them.

Reverse-engineering a causal graph

In our paper, Characterization and Learning of Causal Graphs with Latent Variables from Soft Interventions, we investigate a general scenario where multiple observational and experimental distributions are available, and where the experimental distributions are obtained under soft interventions.

We introduce a new notion of interventional equivalence for causal DAGs with latent node variables. This notion defines when two causal DAGs are indistinguishable from the available data under the latter constraints. Accordingly, we devise the first graphical characterization for two causal DAGs with latents to be interventionally equivalent. Finally, we formulate a sound algorithm to learn such an equivalence class. Given a set of distributions, the algorithm returns a summary graph that encodes common graphical properties of all the causal DAGs that are interventional equivalent.

What’s most interesting is that we find that a soft intervention modifies the mechanisms of the intervened variables in the data generating model without eliminating any cause.

We observe the invariances given by conditional independence and its graphical counterpart d-separation represent just one special type of a broader set of constraints, which follow from the careful comparison of the different distributions available, and those constraints are intrinsically connected with the celebrated do-calculus.

In other words, we can reverse engineer the underlying causal graph, up to the equivalence class, using do-calculus rules of converse direction. Thus, do-constraints provide an interventional equivalent in class characterization.

Discussion

One of the most challenging aspects of this work was that the graphical characterization proof was non-trivial and required us to show that graphical separation statements have some structure that some can be written as deterministic functions of others, which allowed the proof.

The completeness of the learning algorithm is still an open problem. In other words, it is unclear at this point if we can (or cannot) orient more edges in the summary graph which would encode common graphical properties for all the causal DAGs in the equivalence class.

Ultimately, it was a nice surprise discovering that, even in the presence of latent variables, it is possible to represent the interventional equivalence class using a single graph, once we restrict ourselves to soft interventions.