Like scaling mountains, deep learning requires massive amounts of energy. To reach the correct destination in the shortest amount of time with the least amount of energy, we develop optimization techniques. Gradient clipping is one such technique. Though it is widely used in language models, to date it lacks a strong theoretical grounding and this limits its potentially broader impact. In our paper, Why Gradient Clipping Accelerates Training, selected for oral presentation in ICLR 2020, we provide a new theoretical foundation, supported by experiments, for why indeed for gradient clipping accelerates gradient descent for non-smooth non-convex functions.

Solving the mystery of why adaptive methods converge fast

We study optimization algorithms for neural network training and aim to resolve the mystery of why adaptive methods converge fast. Much progress has been made to close the gap between upper and lower oracle complexities for first order smooth optimization. The works dedicated to this goal provide important insights and tools for us to understand the optimization procedures. However, there is another gap that separates theoretically accelerated algorithms from empirically fast algorithms. Our work aims to close this gap.

We analyze a simple but increasingly popular optimization technique known as gradient clipping, which addresses the problem of “exploding gradients” especially common in Recurrent Neural Networks. Others have discussed the gradient explosion problem in recurrent models and consider clipping as an intuitive work around. The technique is default in repos such as AWD-LSTM training, Proximal policy gradient, BERT-pretraining, and others. Our contribution is to formalize this intuition with the theoretical foundation. Based on this clearer theoretical view, we propose a new algorithm called clipped GD which provably converges faster than fixed-step gradient descent.

Smoothness is the key

The key ingredient is a new smoothness condition derived from practical neural network training examples. Smoothness is a concept central to the analysis of first-order optimization algorithms and (under the usual Lipschitz assumption) it is often assumed to be a constant. It turns out, this assumption is very weak. Smoothness actually demonstrates significant variability along the training trajectory of deep neural networks. Moreover, smoothness is often positively correlated with gradient norm and, contrary to standard assumptions in the literature, it can grow with the norm of the gradient.

We therefore introduce clipped GD with a relaxed smoothness assumption, along with the following theorems for which the algorithm holds:

We provide a convergence rate for clipped GD under our new smoothness assumption (Theorem 3).
We prove an upper-bound (Theorem 6) and a lower-bound (Theorem 4) on the convergence rate of GD under our relaxed smoothness assumption. The lower-bound demonstrates that GD with fixed step size can be arbitrarily slower than clipped GD.
We provide upper bounds for stochastic clipped GD (Theorem 7) and SGD (Theorem 8). Again, stochastic clipped GD can be arbitrarily faster than SGD with a fixed step size.
We prove an upper-bound (Theorem 6) and a lower-bound (Theorem 4) on the convergence rate of GD under our relaxed smoothness assumption. The lower-bound demonstrates that GD with fixed step size can be arbitrarily slower than clipped GD.
We provide upper bounds for stochastic clipped GD (Theorem 7) and SGD (Theorem 8). Again, stochastic clipped GD can be arbitrarily faster than SGD with a fixed step size.

The Math

First, we make the following assumptions to regularize the function class studied:

The function 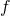$f$ is lower bounded by $f^* > -\infty$ .
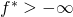The function 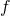$f$ is twice differentiable.
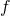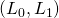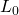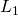The function $f$ is $(L_0,L_1)$ -smooth, i.e., there exist positive constants $L_0$ and $L_1$ such that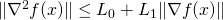 $\|\nabla^2 f(x)\| \le L_0 + L_1\|\nabla f(x)\|$

Now let’s begin with the updated clipped GD algorithm. For the clipped GD, let $\mathcal{F}$ denote the class of functions that satisfy the aforementioned assumptions in set $\mathcal{S}$ defined in the paper. Recall $f^*$ is a global lower bound for function value. With $\eta_c = \tfrac{1}{10L_0}, \gamma = \min\{\tfrac{1}{\eta_c}, \tfrac{1}{10 L_1 \eta_c}\},$ we can prove that the iteration complexity of clipped GD is upper bounded by

$\frac{20L_0(f(x_0)-f^*)}{\epsilon^2} + \frac{20\max\{1, L_1^2\}(f(x_0)-f^*)}{L_0}\ \ \text{.}$

Now, we discuss the convergence of vanilla GD. We will show below that gradient descent is suboptimal under our relaxed smoothness condition. In particular, to prove the convergence rate for gradient descent with fixed step size, we need to permit it benefit from an additional assumption on gradient norms.

We begin with the following assumption: given an initialization $x_0$ , we assume that

$M := \sup\{\|\nabla f(x)\|\ |\ x\ \text{such that}\ f(x) \le f(x_0) \} < \infty.$

This assumption is in fact necessary, as our next theorem reveals. Let $\mathcal{F}$ be the class of objectives satisfying the aforementioned assumptions with fixed constants $L_0 \ge 1$ , $L_1 \ge 1$ , $M > 1$ . The iteration complexity for the fixed-step gradient descent algorithms parameterized by step size $h$ is at least

$\frac{L_1M(f(x_0)-f^* - 5\epsilon/8)}{8\epsilon^2(\log M + 1)}.$

Lastly, suppose certain hold in set $\mathcal{S}$ . If we pick parameters such that $h = \frac1{(2(ML_1 + L_0))}$ , then we can prove that the iteration complexity of GD with a fixed step size defined in gradient descent is upper bounded by

$4(ML_1 + L_0)(f(x_0) - f^*)\epsilon^{-2}.$

Summary

A broken clock is right twice a day. Without theory underpinning empirical observations, it is difficult to operate effectively when building AI models. We are pleased to make this theoretical contribution to the community in support of making AI models more efficient, and therefore more practical for real-world use.

There is still much to be explored in this direction. First, though our smoothness condition relaxes the usual Lipschitz assumption, it is unclear if there is an even better condition that also matches the experimental observations while also enabling a clean theoretical analysis. Second, we only study convergence of clipped gradient descent. Studying the convergence properties of other techniques such as momentum, coordinate-wise learning rates (more generally, preconditioning), and variance reduction is also interesting. Finally, the most important question is: can we design fast algorithms based on relaxed conditions that achieve faster convergence in neural network training? We intend to explore this in our future work.

For a fuller explanation of gradient clipping and exploding gradients, here is a nice breakdown from Machine Learning Mastery.

Please cite our work using the BibTeX below.

@inproceedings{zhang2019gradient,
title={Why Gradient Clipping Accelerates Training: A Theoretical Justification for Adaptivity},
author={Zhang, Jingzhao and He, Tianxing and Sra, Suvrit and Jadbabaie, Ali},
booktitle={International Conference on Learning Representations},
year={2019}
}