Research

ZO-AdaMM: Derivative-free optimization for black-box problems

Optimization

Cite Download Paper Code

Authors

Xiangyi Chen
Sijia Liu
Kaidi Xu
Xingguo Li
Xue Lin
Mingyi Hong
David Cox

Edited by

Mark Weber

Published on

12/10/2019

Toward derivative-free ZO algorithms

Among algorithms for optimizing neural networks, gradient descent is the predominant class. Where the purpose of optimization is to find the weights (W) that minimize the loss function, a gradient defines the vector of slopes (i.e. the derivative) representing the shortest path toward that objective. By analogy: the steepest part of the hill allows you to descend most quickly to the bottom where a treasure chest of W’s sits.

The problem is, gradient descent can be very expensive or even impossible, in certain settings such as in high dimensionality. Enter gradient-free, or zeroth-order (ZO) optimization methods.

Zeroth-order (ZO) optimization methods can be used to solve problems in which there are complex data generation processes that can’t be described by analytical forms but can provide function evaluations, such as measurements from physical environments or predictions from privately deployed machine learning and deep learning models. Handling optimization for these types of problems falls into zeroth-order (ZO) optimization with respect to black-box models, where explicit expressions of the gradients are difficult to compute or infeasible to obtain.

Different from the conventional gradient-based first-order (FO) algorithms, ZO suffers from larger convergence error but still obeys the descent property as the FO method toward a stationary point of nonconvex problems in general. In Figure 1 below, we provide a visualization on the comparison between FO stochastic gradient descent (SGD) and ZO-SGD.

Stogastic gradient descent versus zeroth-order SGD

First-Order Stochastic Gradient Descent versus Zeroth-Order Deritative-Free optimization.

Introducing the derivative-free ZO-AdaMM method

In our paper, ZO-AdaMM: Zeroth-Order Adaptive Momentum Method for Black-Box Optimization, presented at NeurIPS 2019, we provide the theoretical and empirical grounding for a first-of-its-kind method bridging the fields of gradient-free ZO algorithms and adaptive gradient algorithms that take momentum into account.

ZO-AdaMM enjoys the dual advantages of momentum and adaptive learning rates even in the absence of first-order information. We prove its convergence and demonstrate its effectiveness in generating per-image and universal black-box adversarial attacks. As a bonus, we also show for the first time how Euclidean projection-based adaptive gradient methods could suffer non-convergence issues for non-convex constrained optimization.

One of the interesting challenges we faced in our theoretical analysis was how to achieve a tight dependency on the dimension of the problem by leveraging its high dimensional geometry (see the paper to learn more). We’re excited about the theoretical foundation provided in the paper as well as the experimental results, which surpass state-of-the-art methods by quite a measure.

How ZO-AdaMM works

ZO-AdaMM is a gradient-free variant of AMSGrad, which is a modified version of the Adam algorithm with convergence guarantees for both convex and nonconvex optimization. ZO-AdaMM solves black-box stochastic optimization problems of the generic form,

$\min_{\mathbf x \in \mathcal X} f(\mathbf x)=\mathbb{E}_{\boldsymbol \xi}[f(\mathbf x; \boldsymbol{\xi })],$

where $\mathbf x \in \mathbb R%d$ is the d-dimensional optimization variable, $\mathcal X$ is the closed convex set, $f$ is a black-box (probably nonconvex) objective function, and $\boldsymbol \xi$ is a certain random variable that captures environmental uncertainties.

Due to the black-box nature of the objective function f, we estimate the value of its gradient by the forward difference of two function values, resulting in the ZO gradient estimate:

$\hat{\nabla}f (\mathbf x ) = % \frac{d}{q\mu} \sum_{i=1}^q \left \{ [ f ( \mathbf x + \mu \mathbf u_i ) - f ( \mathbf x )] \mathbf u_i \right \}, { (d/\mu) [ f ( \mathbf x + \mu \mathbf u ) - f ( \mathbf x ) ] } \mathbf u$

where $\mathbf u$ is a random unit direction vector, and $\mu$ is a small smoothing parameter.

By leveraging ZO gradient estimates, ZO-AdaMM updates the optimization variable $\mathbf x$ by using the adaptive learning rate and the momentum-type descent direction. Formally, the ZO-AdaMM algorithm is of the following form:

Zo-AdaMM algorithm

Convergence of ZO-AdaMM

Our work provides the theoretical analysis of the convergence of ZO-AdaMM for both unconstrained and constrained nonconvex optimization. Roughly speaking, under a set of mild conditions, ZO-AdaMM converges to a stationary point in the sub-linear convergence rate. There exist two key factors that guarantee the convergence of ZO-AdaMM:

Mahalanobis distance based projection operation
The boundedness of the 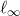$\ell_{\infty}$ norm of a ZO gradient estimate

For (1), we theoretically show that the convergence of ZO-AdaMM is benefited from the use of Mahalanobis distance based projection operation. If the Euclidean distance (rather than the Mahalanobis distance) was used, then the algorithm may diverge. Spurred by that, our work proposes a Mahalanobis based convergence measure to facilitate the convergence analysis of ZO-AdaMM.

For (2), in order to derive a tight convergence rate of ZO-AdaMM, it requires to examine the boundedness of each coordinate of a ZO gradient estimate. Our work shows that as the as long as the number of iterations T has polynomial rather than exponential dependency on the problem size d, the $\ell$ norm of a ZO gradient estimate can be bounded as,

$\max_{t\in [T]} \{ \| \hat{\mathbf g}_t \|_\infty \} = O(\sqrt{d\log{(d)}})$

ZO-AdaMM for Adversarial Machine Learning

Our work demonstrates the effectiveness of ZO-AdaMM by experiments on generating adversarial examples from black-box neural networks, whose internal configurations are not accessed by the adversary.

Here we focus on two types of black-box adversarial attacks:

1. Per-image adversarial perturbation
2. Universal adversarial perturbation against multiple images

For each type of attack, we allow both constrained and unconstrained optimization problem settings. We compare our proposed ZO-AdaMM method with 6 existing ZO algorithms: ZO stochastic gradient descent (ZO-SGD), ZO stochastic coordinate descent (ZO-SCD) and ZO sign-based SGD (ZO-signSGD) for unconstrained optimization, and ZO projected SGD (ZO-PSGD), ZO stochastic mirror descent (ZO-SMD) and ZO-NES for constrained optimization.

Figure 2: Generating adversarial perturbation (attack) from a (black-box) convolutional neural network (CNN)

In the example of per-image adversarial perturbation, ZO-AdaMM consistently outperforms other ZO methods in terms of the fast convergence of attack loss and relatively consumed small perturbation. This conclusion is consistent in the application of generating universal perturbation when we attack 100 randomly selected ImageNet images simultaneously. ZO-AdaMM has the fastest convergence speed to reach the smallest adversarial perturbation required for successful adversarial attacks.

Figure 2.1 Unconstrained setting for the attack loss and adversarial distortion v.s. iterations. Each box represents results from 100 images.*

Figure 2.2. Constrained setting

By visualizing the generated universal adversarial perturbations (Figure 3), the fast convergence of ZO-AdaMM leads to a more imperceptible perturbation pattern to reach the targeted misclassification.

Figure 3: The attack loss and adversarial distortion vs. iterations. Each box represents results from 100 images.

In Figure 4 below, we show the visualization of universal perturbation versus different iterations and the eventually generated adversarial examples. The left four columns present universal perturbations found by different ZO algorithms at the iteration number 1000, 5000, 10000 and 20000, where the depth of the color corresponds to the strength of the perturbation, and the maximum distortion (with deepest green) is given at the bottom of each subplot. The right four columns are 4 of 10 adversarial examples that lead to misclassification from the original label ‘brambling’ to an incorrectly predicted label given at the bottom of each subplot.

Figure 4: Visualization of universal perturbation versus different iterations and the eventually generated adversarial examples.

Reflection

One thing we focused on in this paper was providing a strong theoretical foundation to along with the empirical results.

Theoretically, we provided the first convergence analysis of ZO algorithms that take into account momentum and adaptive learning rates. This is also the first time to theoretically show that the Euclidean projection based adaptive gradient-type methods could suffer non-convergence issues for constrained optimization.

Practically, we formalized the experimental comparison of ZO-AdaMM with 6 state-of-the-art ZO algorithms in the application of black-box adversarial attacks to generate both per-image and universal adversarial perturbations. This could provide an experimental benchmark for future studies on ZO optimization.

Please cite our work using the BibTeX below.

@misc{chen2019zoadamm,
title={ZO-AdaMM: Zeroth-Order Adaptive Momentum Method for Black-Box Optimization},
author={Xiangyi Chen and Sijia Liu and Kaidi Xu and Xingguo Li and Xue Lin and Mingyi Hong and David Cox},
year={2019},
eprint={1910.06513},
archivePrefix={arXiv},
primaryClass={cs.LG}
}