Causal inference is expensive. Here’s an algorithm for fixing that.
Authors
Authors
- Kristjan Greenewald
- Murat Kocaoglu
- Sara Magliacane
- Dmitriy Katz
- Karthikeyan Shanmugam
- Enric Boix-Adsera`
- Guy Bresler
Edited by

Authors
- Kristjan Greenewald
- Murat Kocaoglu
- Sara Magliacane
- Dmitriy Katz
- Karthikeyan Shanmugam
- Enric Boix-Adsera`
- Guy Bresler
Edited by
Published on
12/08/2019
Categories
Does eating chocolate make you smarter? In a 2012 study published in the New England Journal of Medicine, researchers note a striking correlation between chocolate consumption and Nobel prizes per capita, prompting the idea that perhaps chocolate improves cognitive functioning. Understanding cause and effect is fundamental to intelligence, from the tiniest organisms to the highest orders of human reasoning. But we often make mistakes, confusing correlation and causality. Learning true cause-and-effect relationships is difficult. We can only do so through many trials (interventions) controlling for every possible variable, but this is very expensive. In our paper, Sample Efficient Active Learning of Causal Trees, published in NeurIPS 2019, we propose an intervention design method called the Central Node Algorithm to make causal learning more efficient, and therefore more practical.
Active learning and causal discovery
An active learning algorithm is one that actively engages some subject or information source. It is the computer science equivalent of statistical experiment design, a real-world example of which might be a Randomized Control Trial (RCT) to study whether or not chocolate really does improve cognition.
Active learning is popular for problems in which data is abundant but labels are scarce or expensive because the algorithm can interact with the data to generate labels.
In the case of a causal model, which can be described as a graph of nodes and edges mapping cause and effect relationships, we want to see if we can use active learning to learn the directed edges of a causal graph. Ideally, this is done by iteratively using current knowledge to design targeted experiments (interventions) in the system that result in causal structure being learned as quickly as possible.
It turns out that in this regime the common active learning approach of greedily choosing interventions that maximize information gain
can be shown to be exponentially suboptimal in terms of the number of interventions required to learn causal relationships (see figure below).
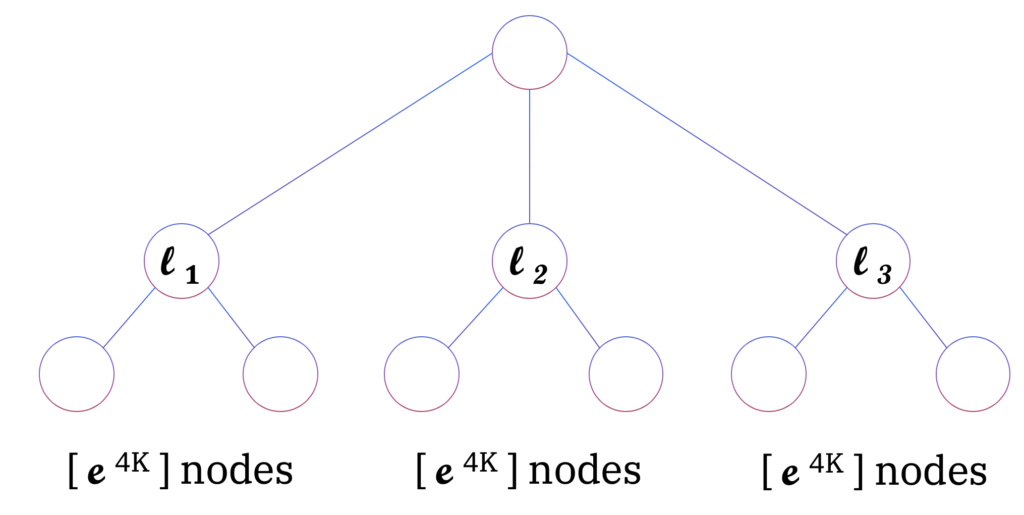
A greedy active learning algorithm, shown for K = 3. The optimal algorithm can find the root in [log2 K] + 1 interventions by a top-down approach, while the information greedy algorithm intervenes on the lk (k = 1, …, K) nodes, taking at least K / 2 steps in expectation.
Central Node Algorithm
We propose an intervention design method called the Central Node Algorithm that overcomes this exponential suboptimality.
In fact what’s exciting about this algorithm is that it is provably near optimal for iterative experiment design when orienting the edges in a causal graph whose un-oriented components form a forest. This means we can now give active learning agents the ability to efficiently explore an environment and discover its causal structure.
How it works
Consider the problem of experimental design for learning causal graphs that have a tree structure. Using an adaptive framework we can determine the next intervention based on a Bayesian prior updated with the outcomes of previous experiments, focusing on the setting where observational data is cheap (assumed infinite) and interventional data is expensive.
In this setting, we show that the algorithm requires a number of interventions less than or equal to a factor of 2 times the minimum achievable number. Additionally, several extensions are presented, to the case where a specified set of nodes cannot be intervened on, to the case where K interventions are scheduled at once, and to the fully adaptive case where each experiment yields only one sample. In the case of finite interventional data, through simulated experiments we show that our algorithms outperform different adaptive baseline algorithms.
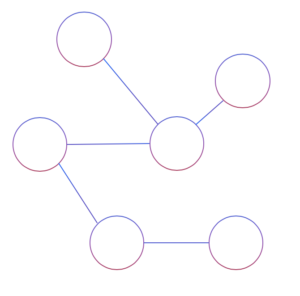
Step 1: Observed data with undefined causal relationships
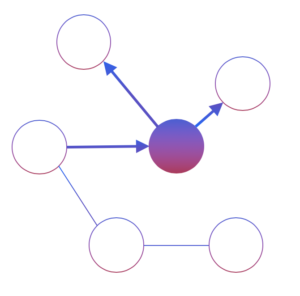
Step 2: Intervene on a central node to reveal its causal edges
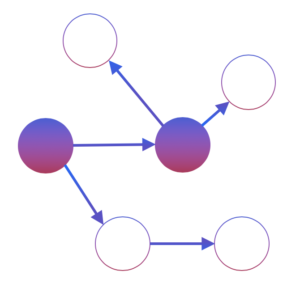
Step 3: Repeat until all edges are mapped
Reflection
One of the surprises in our work was the fact that we can prove that the performance of our approach is close to that of the (unknown) optimal algorithm.
Moreover, the exploration problem is particularly intriguing since the algorithm that greedily maximizes information gain (a popular approach in active experiment design) can take exponentially longer to orient the graph than our approach does.
As this research develops, we could see similar concepts being used to design AI agents that when asked to operate in an environment. In such a setting, an agent first adaptively explores the environment with targeted experimentation to build a causal model, then uses this causal model to reason about how to best go about completing tasks it is asked to do. Then the agent may also make sense of the behavior of other (possibly non-artificial) agents and predict the future state of the system. Such capabilities are fundamental to all forms of intelligence, and we are beginning to take small steps toward this with causal inference algorithms.
Causal inference is an important line of work at the MIT-IBM Watson AI Lab. Also see our NeurIPS 2019 paper, Characterization and Learning of Causal Graphs with Latent Variables from Soft Interventions.
Please cite our work using the BibTeX below.
@incollection{NIPS2019_9575,
title = {Sample Efficient Active Learning of Causal Trees},
author = {Greenewald, Kristjan and Katz, Dmitriy and Shanmugam, Karthikeyan and Magliacane, Sara and Kocaoglu, Murat and Boix Adsera, Enric and Bresler, Guy},
booktitle = {Advances in Neural Information Processing Systems 32},
editor = {H. Wallach and H. Larochelle and A. Beygelzimer and F. d\textquotesingle Alch\'{e}-Buc and E. Fox and R. Garnett},
pages = {14279--14289},
year = {2019},
publisher = {Curran Associates, Inc.},
url = {http://papers.nips.cc/paper/9575-sample-efficient-active-learning-of-causal-trees.pdf}
}